
#Gauss seidel program in scilab update
Step 2: Set ϕ ( n+1) = ϕ ( n) and apply the Gauss–Seidel update formula, Eq. If any of the boundaries have Dirichlet boundary conditions, the guessed values for the boundary nodes corresponding to that boundary must be equal to the prescribed boundary values. Step 1: Guess values of ϕ at all nodes, i.e., ϕ i, j ∀ i = 1. In general, the update formula for the Gauss–Seidel method may be written as Essentially, this implies that only two out of the four terms on the right-hand side of the update formula are treated explicitly, as shown in Fig. 3.3(a), then, by the time it is node O’s turn to get updated, nodes W and S have already been updated, and these updated values must be used. In the context of solution of a 2D PDE on a structured mesh, if the node by node update pattern (or sweeping pattern) is from left to right and bottom to top, as shown in Fig. For x, the most recent value, which happens to be the current iteration value (since it has already been updated), is used. (3.17b), only z assumes a previous iteration value. (3.17a), both y and z assume previous iteration values. Thus, for the 3×3 example system considered earlier when x is determined using Eq. (3.31), whenever an updated value becomes available, it is immediately used. In the Gauss–Seidel method, instead of always using previous iteration values for all terms of the right-hand side of Eq.

The Gauss–Seidel method is also a point-wise iteration method and bears a strong resemblance to the Jacobi method, but with one notable exception. However, as the level of convergence can be set by the users, a lower precision may be desired in order to detect the potential trend of the changing design variables much quicker than the direct method can provide. On the other hand, the indirect method reaches the final solution gradually. In summary, the direct method requires more in-core computer memory, but the solutions are accurate. As seen in the two iterative procedures shown above, iterative methods slowly reach the final solution rather than a large final step, as seen in the backward substitution procedures of the Gauss elimination. Thus, no further discussion is made regarding other iterative solvers. Other iterative procedures apply different and yet conceptually similar approaches. On the other hand, the Gauss–Seidel method can replace each variable as soon as a new update becomes available. As such, all variables need to be stored in memory until the iteration is finished. In terms of computational efficiency, the simultaneous displacement (Jacobi) method is perfectly designed for parallel computing, because none of the variables within each iteration change until the iteration is completed. Although this is true in most problems, some special cases may have opposite results.
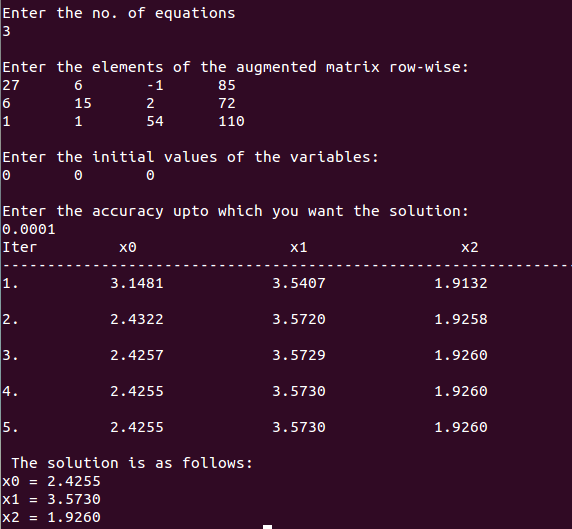

Convergence processes of using the Gauss–Seidel iterative procedures for the 4-node, 3-element bar problem.Ĭomparing results obtained from the Jacobi and Gauss–Seidel methods for this particular example problem, we observed that the convergence occurs much quicker for the Gauss–Seidel method.


 0 kommentar(er)
0 kommentar(er)
